In a downlink networking system, the base station (BS) is the one who manages and allocates resources to users. These resources typically include frequency bands, transmission power, time slots, and other related parameters. So a key aspect for BS to consider is efficient way of utilizing networking resources. In other words, since networking resources are limited, it is important to manage these resources efficiently to ensure high throughput data transmission.

While there are multiple networking techniques to handle resources, in this page we’ll be briefly discussing the Non-Orthogonal Multiple Access (NOMA). And it is essential to know what Orthogonal Multiple Access (OMA) is.

Orthogonal Multiple Access (OMA)

OMA is a wireless communication technique where the communication resources are allocated orthogonally to users. What “orthogonal” resource allocation means is that resources such as frequency, power, or time are assigned exclusively to users, in order to prevent interference between the users.

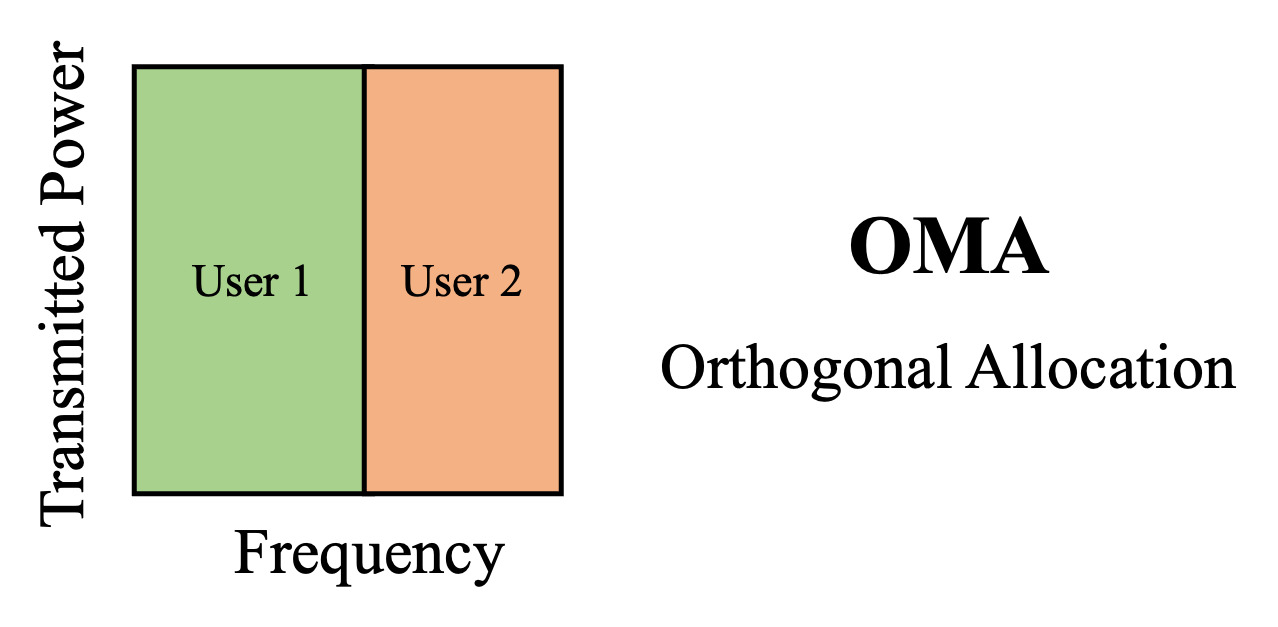
Figure 1. OMA Basic

Non-Orthogonal Multiple Access (NOMA)

And the Non-Orthogonal Multiple Access (NOMA) is a more advanced which enhances spectral efficiency. It allows multiple users to share the same frequency band and time slots simultaneously. The key difference between NOMA and OMA lies here: instead of separating users orthogonally, NOMA differentiates users in power level. It assigns different power to users based on their channel condition, such as distance between user and BS or noise ratio.

Let’s take a look at the following example, shown in Figure 2.

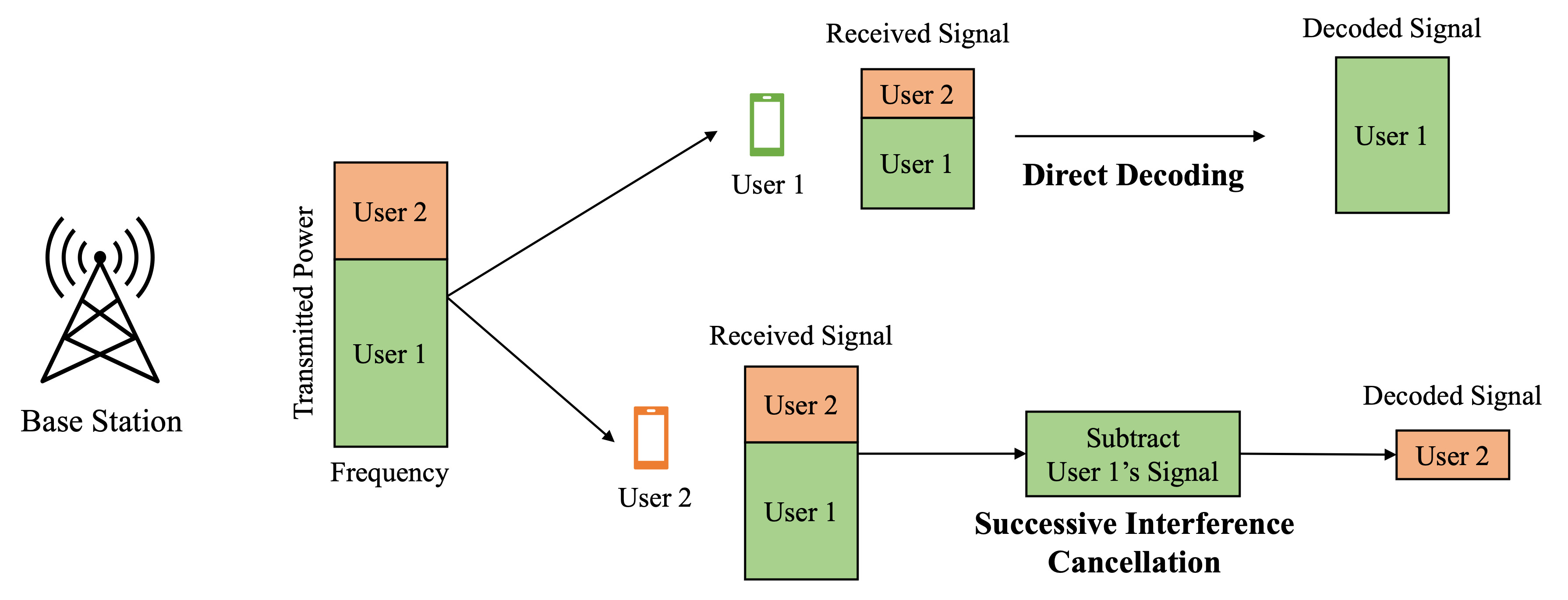
Figure 2. NOMA Basic

Suppose there are two users, User 1 and User 2. The distance between the BS and the users differs, such that User 1 is farther while User 2 is closer.

Since User 1 is farther from the base station than User 2, it is likely that User 1’s signal will be more affected by noise. Due to this, the receiver may not be able to successfully decode User 1’s data. Therefore, the BS’s job is to assign more transmission power to User 1 than to User 2. This power allocation ensures successful transmission of weaker users’ data, such as User 1’s, even under poor channel conditions.

From the weaker user’s perspective, in this case User 1 the decoding process is quite simple. Since User 1’s signal dominates, in terms of power, the received data can be directly decoded by treating User 2’s lower-power signal as noise.

On the other hand, for stronger users, User 2, the receiver cannot tell the difference between the users within the same frequency band. o enable the stronger user’s receiver to distinguish between signals between User 1 and User 2, Successive Interference Cancellation (SIC) is employed, which works by leveraging the difference in received power levels. What SIC essentially does is subtracting the weaker user’s signal from the received data. After cancellation, the receiver can decode its own signal.

Basic Notations

  • \(n\)th user
  • \(k\)th channel
  • \(N_k\): total number of users using \(k\)th channel
  • \(z^k_n\): additive white Gaussian noise (AWGN)
  • \(B_{total}\): total bandwidth
  • \(K\): total number of channels
  • \(N\): total number of users
  • \(B_c=B_{total}/K\): divided bandwidth by channels

Channel to Noise Ratio (CNR)

CNR is a ratio between the power of the carrier signal (channel) and the power of the noise.

\[\begin{align} \Gamma_n^k &= g^o_{n, k} \\ &= \frac{|h^k_n|^2}{\sigma^2_{z_k}} \\ \end{align}\]
  • \(h^k_n\): channel response between BS and \(n\)th user which considers both the path loss \(\mathcal{P}_L\) and shadowing effect \(h'_{n, k}\) (= Rayleigh fading)
  • \(\sigma^2_{z_k}\): variance of AWGN

Signal to Noise plus Interference Ratio (SINR)

NOTE: An assumption behind the following equations is;

\[\Gamma^k_1 > ... > \Gamma^k_n > ... > \Gamma^k_{N_k}.\]

This means that the 1st user and the last user has the strongest and lowest signal power respectively. According to NOMA protocol, users with lower CNR will be assigned with more power.

\[p^k_1 < p^k_2 < ... < p^k_n < ... < p^k_{N_k},\]

where \(p^k_n\) denotes transmit power of user \(n\) using channel \(k\).

Due to the characteristic of successive interference cancellation (SIC), an user will treat less power as an interference and decode signals of more power.

\[\begin{align} \gamma_{n}^{k} &= \frac{p_n^k \Gamma_n^k}{1 + \sum_i^{n-1}{p_i^k \Gamma_n^k}} \\ &= \frac{P_{n, k}(t) \mathcal{P}_L(d)|h'_{n, k(t)}|^2}{n^2_0 + \sum_{i=1}^{n-1}{P_{n, k}(t) \mathcal{P}_L(d)|h'_{n, k(t)}|^2}} \end{align}\]
  • \(d\): distance between BS and user \(n\) which is using channel \(k\)
  • Typically, \(n^2_0\) and \(1\) represents a constant noise term.
  • Equation (2) is from TPPD paper.

Overall, SINR is to calculate the ratio between received power (numerator) and other noises and interferences (denominator) which comprises noises (1 or \(n^2_0\)) and interferences (sum of other users’ received power).

Take the numerator, by multiplying the allocated power and CNR (\(p^k_n \Gamma^k_n\)), this results a signal power considering the noise.

And now let’s take a look at the denominator. The 1 denotes the noise and \(\sum_i^{n-1}p^k_i\Gamma^k_n\) is to sum all the signal powers which are less than \(p^k_n\) (take a look at the NOTE assumption).

By dividing the above two, ratio of signal power versus noises can be calculated.

Data Rate

\[R^k_n(\Gamma^k_n, p^k_1, ..., p^k_n) = B_c\log_2{(1+\frac{p^k_n \Gamma^k_n}{1+\sum_{i=1}^{n-1}p^k_i\Gamma^k_n})}.\]
  • \(\frac{p^k_n \Gamma^k_n}{1+\sum_{i=1}^{n-1}p^k_i\Gamma^k_n}\): As described above, this term represents SINR.
  • \(1 + \frac{p^k_n \Gamma^k_n}{1+\sum_{i=1}^{n-1}p^k_i\Gamma^k_n}\): By adding 1 to SINR, it can prevent logarithm taking zero.
  • \(\log_2{(1+\frac{p^k_n \Gamma^k_n}{1+\sum_{i=1}^{n-1}p^k_i\Gamma^k_n})}\): The term calculates the achievable data rate for a noisy channel and it’s derived from Shannon capacity formula.
  • \(B_c\log_2{(1+\frac{p^k_n \Gamma^k_n}{1+\sum_{i=1}^{n-1}p^k_i\Gamma^k_n})}\): Shannon capacity formula, providing an upper bound on the achievable data rate for a given channel. By multiplying the bandwidth (Hz) and achievable data rate, data rate for the given bandwidth is calculated.

According to the above, two users’ data rate can be derived as such:

\[\begin{align} R^k_1(\Gamma^k_1, p^k_1, p^k_2) &= B_c\log_2{(1+p^k_1\Gamma^k_1)} \\ R^k_2(\Gamma^k_2, p^k_1, p^k_2) &= B_c\log_2{(1+ \frac{p^k_2\Gamma^k_2}{1+p^k_1\Gamma^k_2})}. \end{align}\]

Maximizing Sum Rate (MSR)

Let \(A^k_n=2^{\frac{(R^k_n)_{min}}{B_c}}\) and assume \(A^k_2\geq 2.\)

Derivation of \(A^k_n\): Let us assume there is a power \(p'\) which ends up with a minimum data rate \((R^k_n)_{min}\).

\[\begin{align*} (R^k_n)_{min} \triangleq B_c\log_2{(1 + \frac{p'\Gamma^k_n}{1+\sum^{n-1}_{i=1}p'\Gamma^k_n})} \end{align*}\]

For the sake of simplicity, let’s say the term inside the logarithm as \(P'\), achievable minimum data rate. Then the above equation can be rewritten as

\[2^{\frac{(R^k_n)_{min}}{B_c}}=P'=A^k_n.\]

MSR is an objective function to ensure the total throughput to be maximized; you can easily consider the MSR metric when the \(\alpha\)-fairness function is in the condition of \(\alpha=1\).

For MSR, the power allocation problem is formulated as

\[\begin{align} \max_{P} &\sum_{k=1}^{K}[R^k_1(p^k_1, p^k_2) + R^k_2(p^k_1, p^k_2)], \\ \text{subject to } & R^k_n \geq (R^k_n)_{min}, n=1, 2, \forall k = 1, ..., K, \\ & \sum_{k=1}^K(p^k_1 + p^k_2)\leq P_T, \\ & 0 \leq p^k_1\leq p^k_2, \forall k=1, ..., K. \end{align}\]

As MSR the term itself describes, the problem is to maximize the sum rate, in other words data rate. MSR’s final objective is to find an optimal power for user 1 and 2.

Here, let’s say there is a power limit of \(q_k=p^k_1+p^k_2\), meaning that total allocated power of \(k\)th channel should be \(q_k\). Then the solution for the MSR is

\[\begin{align} p^k_1 &= \frac{q_k\Gamma^k_2 - A^k_2 + 1}{A^k_2\Gamma^k_2} \\ p^k_2 &= q_k-p^k_1. \end{align}\]

Maximizing Minimal Rate (MMR)

\[\begin{align} p^k_1 &= \frac{-(\Gamma^k_1 + \Gamma^k_2) + \sqrt{(\Gamma^k_1 + \Gamma^k_2)^2 + 4\Gamma^k_1(\Gamma^k_2)^2q_k}} {2\Gamma^k_1\Gamma^k_2} \\ p^k_2 &= q_k - p^k_1 \end{align}\]