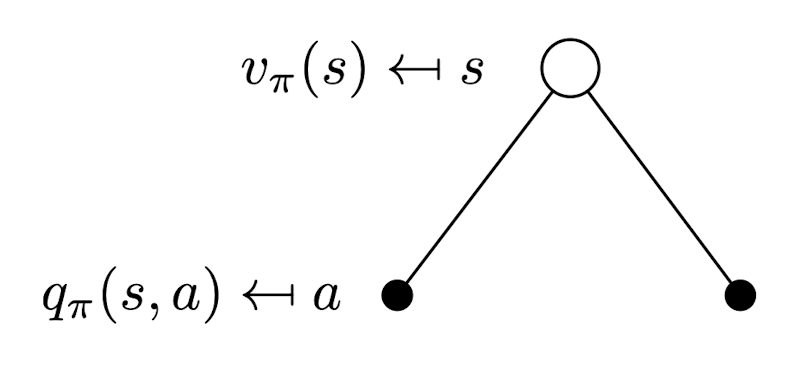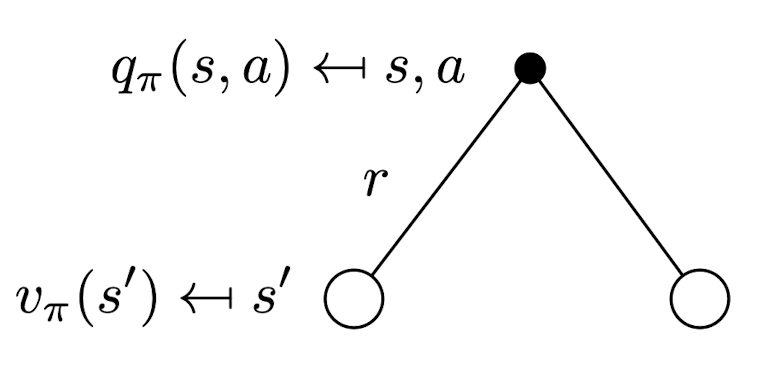Markov Decision Processes
Markov Decision Processes
1. Markov Processes
1.1. Introduction to MDPs
- Markov Decision Processes formally describe an environment for reinforcement learning.
- environment is fully observable
1.2. Markov Property
- the future is independent of the past given the present
Definition
A state \(S_t\) is Markov if and only if \(\mathbb{P}[S_{t+1}|S_t] = \mathbb{P}[S_{t+1}|S_1, ..., S_t]\)
1.3. Markov Chains
Definition
A Markov Process (or Markov Chain) is tuple \((\mathcal{S}, \mathcal{P})\) \(\mathcal{S}\) is a finite set of states \(\mathcal{P}\) is a state transition probability matrix
2. Markov Reward Processes
2.1. Markov Reward Process
Definition
A Markov Reward Process is a tuple \((\mathcal{S}, \mathcal{P}, \mathcal{R}, \mathcal{\gamma})\)
2.2. Return
Definition
\(G_t = R_{t+1} + \gamma R_{t+2} + ... = \sum_{k=0}^{\infty}\gamma^k R_{t+k+1}\) where \(\gamma \in [0, 1]\).
2.3. Value Function
Definition
\(v(s) = \mathbb{E}[G_t |S_t = s]\) e.g.) \(G_1 = R_2 + \gamma R_3 + ... + \gamma^{T-2}R_T\)
2.4. Bellman Equation for MRPs
\[\begin{align*} v(s) &= \mathbb{E}[G_t | S_t = s] \\ &= \mathbb{E}[R_{t+1} + \gamma R_{t+2} + \gamma^{2} R_{t+3} + ... | S_t = s] \\ &= \mathbb{E}[R_{t+1} + \gamma(R_{t+2} + \gamma R_{t+3} + ...) | S_t = s] \\ &= \mathbb{E}[R_{t+1} + \gamma(G_{t+1}) | S_t = s] \\ &= \mathbb{E}[R_{t+1} + \gamma(v(S_{t+1})) | S_t = s] \\ \end{align*}\] 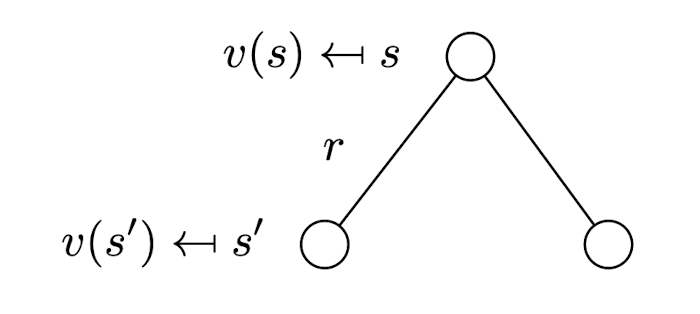
3. Markov Decision Processes
3.1. Markov Decision Process
Definition
A Markov Decision Process is a tuple \((\mathcal{S}, \mathcal{A}, \mathcal{P}, \mathcal{R}, \gamma)\)
3.2. Policies
Definition
\(\pi(a|s) = \mathbb{P}[A_t = a | S_t = s]\)
3.3. Value Function
Definition
state-value function
\(v_\pi (s) = \mathbb{E}[G_t | S_t = s]\)
Definition
action-value function
\(q_\pi(s, a) = \mathbb{E}[G_t | S_t = s, A_t = a]\)
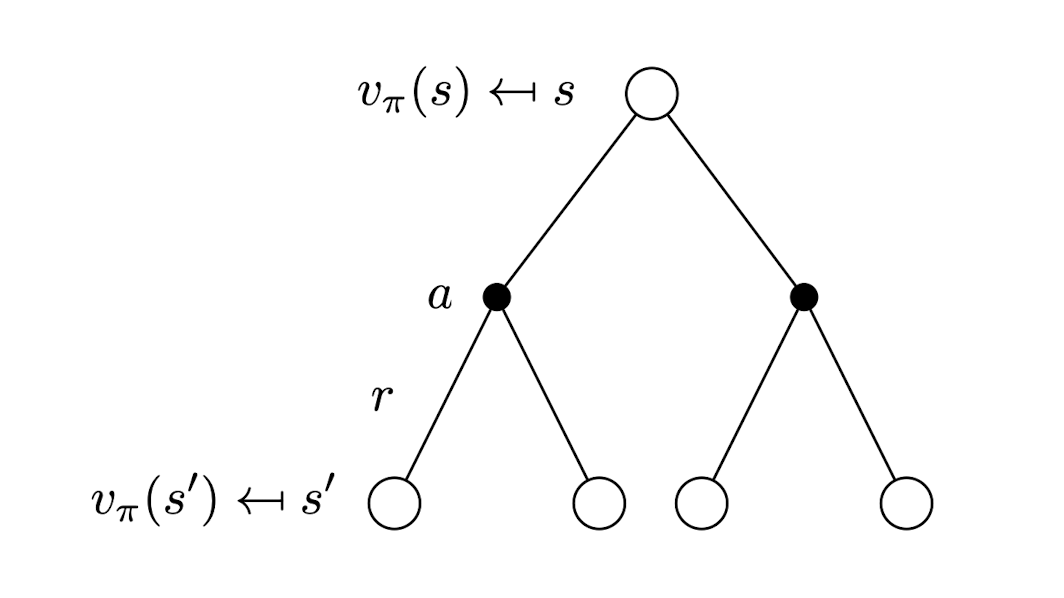
3.4. Bellman Expectation Equation
\[\begin{align*} v_\pi (s) &= \mathbb{E}[G_t | S_t = s] \\ &= \mathbb{E}[R_{t+1} + \gamma v_\pi(S_{t+1}) | S_t = s] \end{align*}\] \[\begin{align*} q_\pi(s, a) &= \mathbb{E}[G_t | S_t = s, A_t = a] \\ &= \mathbb{E}[R_{t+1} + \gamma q_\pi(S_{t+1}, A_{t+1}) | S_t = s, A_t = a] \end{align*}\]